In this blog post, we show how we state the functional correctness of the implementation of the STATIC_CALL instruction in Revm, an implementation of the Ethereum's virtual machine EVM in Rust. This involves running rocq-of-rust to translate the Rust code to the theorem prover Rocq, and then making a proof by refinements until obtaining a specification of the code written in purely functional style, optimized for formal verification. This also proves the code cannot panic, as our specifications are free of panics.
This work was funded by a grant from the Ethereum Foundation, to whom we are thankful, related to the zkEVM Formal Verification Project, to bring more security to the Ethereum ecosystem in general.
Completing this work on Revm and the other main implementations of the EVM, together with a proof of equivalence between them, will enable proving that there cannot be network splits due to nodes disagreeing on the EVM semantics.

General overview
We will step through the three main phases of the translation of Rust to Rocq:
- Translation: from the source Rust code to the THIR intermediate representation in Rocq;
- Link: typechecking and naming resolution of the THIR intermediate representation in Rocq;
- Simulation: handling of the control flow and memory mutations to get a purely functional representation in Rocq.
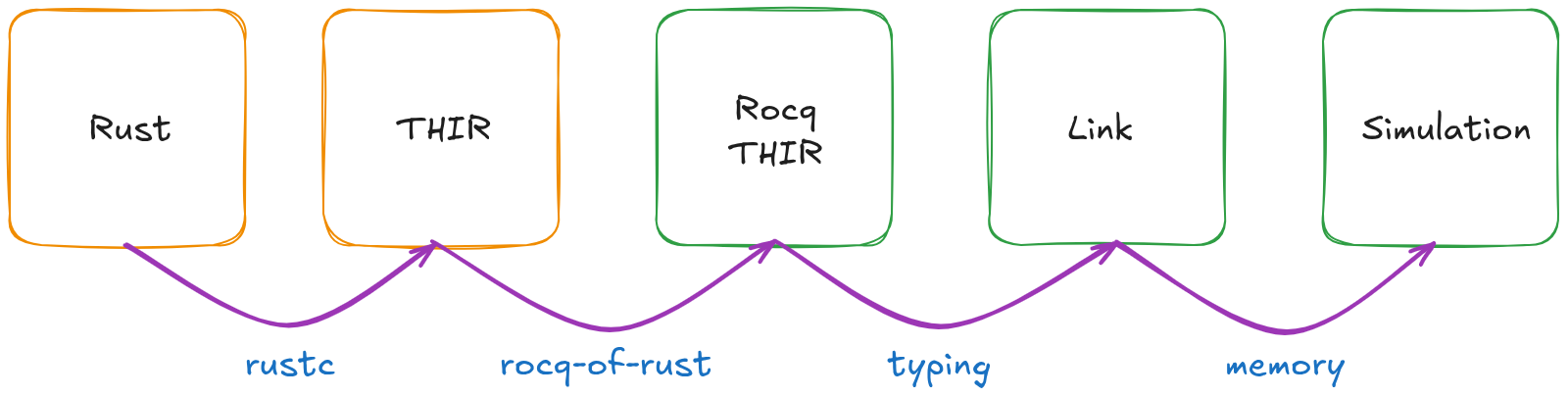
Figure: High-level overview of the translation phases from the source Rust code to a purely functional representation in Rocq.
Source code
Here is the body of the function implementing the STATIC_CALL instruction in Revm, from the file interpreter/src/instructions/contract.rs:
pub fn static_call<WIRE: InterpreterTypes, H: Host + ?Sized>(
interpreter: &mut Interpreter<WIRE>,
host: &mut H,
) {
check!(interpreter, BYZANTIUM);
popn!([local_gas_limit, to], interpreter);
let to = Address::from_word(B256::from(to));
// Max gas limit is not possible in real ethereum situation.
let local_gas_limit = u64::try_from(local_gas_limit).unwrap_or(u64::MAX);
let Some((input, return_memory_offset)) = get_memory_input_and_out_ranges(interpreter) else {
return;
};
let Some(mut load) = host.load_account_delegated(to) else {
interpreter
.control
.set_instruction_result(InstructionResult::FatalExternalError);
return;
};
// Set `is_empty` to false as we are not creating this account.
load.is_empty = false;
let Some(gas_limit) = calc_call_gas(interpreter, load, false, local_gas_limit) else {
return;
};
gas!(interpreter, gas_limit);
// Call host to interact with target contract
interpreter.control.set_next_action(
InterpreterAction::NewFrame(FrameInput::Call(Box::new(CallInputs {
input,
gas_limit,
target_address: to,
caller: interpreter.input.target_address(),
bytecode_address: to,
value: CallValue::Transfer(U256::ZERO),
scheme: CallScheme::StaticCall,
is_static: true,
is_eof: false,
return_memory_offset,
}))),
InstructionResult::CallOrCreate,
);
}
This code contains many difficult parts, including:
- The use of complex traits, such as
InterpreterTypes, relying on associated types and sub-traits; - The use of macros such as
gas!, hiding more code than it appears; - Conversions with inference of the target type, through the use of the
fromandtry_fromfunctions; - A bit of control flow with pattern-matching and early returns.
Here is our specification in Rocq, from the file revm_interpreter/instructions/simulate/contract/static_call.v:
Definition static_call
{WIRE H : Set} `{Link WIRE} `{Link H}
{WIRE_types : InterpreterTypes.Types.t} `{InterpreterTypes.Types.AreLinks WIRE_types}
{IInterpreterTypes : InterpreterTypes.C WIRE_types}
{IHost : Host.C H}
(interpreter : Interpreter.t WIRE WIRE_types)
(host : H) :
Interpreter.t WIRE WIRE_types * H :=
check_macro interpreter SpecId.BYZANTIUM
(fun interpreter => (interpreter, host)) (fun interpreter =>
popn_macro interpreter {| Integer.value := 2 |}
(fun interpreter => (interpreter, host)) (fun arr interpreter =>
let '(_, to, local_gas_limit) := ArrayPairs.to_tuple_rev (arr.(array.value)) in
let to := Impl_Address.from_word (Impl_From_U256_for_FixedBytes_32.from to) in
let local_gas_limit :=
Impl_Result_T_E.unwrap_or
(TryFrom_Uint_for_u64.try_from local_gas_limit)
Impl_u64.MAX in
match call_helpers.get_memory_input_and_out_ranges interpreter with
| (None, interpreter) => (interpreter, host)
| (Some (input, return_memory_offset), interpreter) =>
match IHost.(Host.load_account_delegated) host to with
| (None, host) =>
let control :=
IInterpreterTypes
.(InterpreterTypes.Loop)
.(Loop.set_instruction_result)
interpreter.(Interpreter.control)
instruction_result.InstructionResult.FatalExternalError in
let interpreter :=
interpreter
<| Interpreter.control := control |> in
(interpreter, host)
| (Some load, host) =>
let load := load <| AccountLoad.is_empty := false |> in
match call_helpers.calc_call_gas interpreter load false local_gas_limit with
| (None, interpreter) => (interpreter, host)
| (Some gas_limit, interpreter) =>
gas_macro interpreter gas_limit
(fun interpreter => (interpreter, host)) (fun interpreter =>
let control :=
IInterpreterTypes
.(InterpreterTypes.Loop)
.(Loop.set_next_action)
interpreter.(Interpreter.control)
(interpreter_action.InterpreterAction.NewFrame
(interpreter_action.FrameInput.Call
(Impl_Box.new
{|
call_inputs.CallInputs.bytecode_address := to;
call_inputs.CallInputs.caller :=
InputTraits.target_address interpreter.(Interpreter.input);
call_inputs.CallInputs.gas_limit := gas_limit;
call_inputs.CallInputs.input := input;
call_inputs.CallInputs.is_eof := false;
call_inputs.CallInputs.is_static := true;
call_inputs.CallInputs.return_memory_offset := return_memory_offset;
call_inputs.CallInputs.scheme := call_inputs.CallScheme.StaticCall;
call_inputs.CallInputs.target_address := to;
call_inputs.CallInputs.value := call_inputs.CallValue.Transfer Impl_Uint.ZERO
|}
)))
instruction_result.InstructionResult.CallOrCreate in
let interpreter :=
interpreter <| Interpreter.control := control |> in
(interpreter, host)
) end end end)).
We aim to keep the structure of the Rust code, using the check_macro and popn_macro functions to also reproduce the Rust macros. The added verbosity is essentially due to Rocq notations being heavier, in particular to manipulate structures or to call trait methods, as well as making the state manipulation explicit.
Translation of the THIR
Running the command cargo rocq-of-rust, after installing the tool, automatically extracts the THIR intermediate representation of the Rust code of Revm to Rocq. The representation is typically very verbose, with around 1,000 lines, for example, for the STATIC_CALL function. You can look at the extracted code in revm_interpreter/instructions/contract.v. This is mostly a deep-embedding; it starts like this:
Definition static_call (ε : list Value.t) (τ : list Ty.t) (α : list Value.t) : M :=
match ε, τ, α with
| [], [ WIRE; H ], [ interpreter; host ] =>
ltac:(M.monadic
(let interpreter :=
M.alloc (|
Ty.apply
(Ty.path "&mut")
[]
[ Ty.apply (Ty.path "revm_interpreter::interpreter::Interpreter") [] [ WIRE ] ],
interpreter
|) in
let host := M.alloc (| Ty.apply (Ty.path "&mut") [] [ H ], host |) in
M.catch_return (Ty.tuple []) (|
ltac:(M.monadic
(M.read (|
let~ _ : Ty.tuple [] :=
M.match_operator (|
Ty.tuple [],
M.alloc (| Ty.tuple [], Value.Tuple [] |),
[
fun γ =>
ltac:(M.monadic
(let γ :=
M.use
(M.alloc (|
Ty.path "bool",
M.call_closure (|
Ty.path "bool",
UnOp.not,
To make it understandable, we make a proof by refinement, where we prove in a few steps that the code is equivalent to a simpler version, until arriving at the functional specification.
Typing
Even if the extracted code contains the type annotations from the Rust compiler (the letter T of THIR stands for Type), the extracted code is, for now, untyped, and all the values are in the special type Value.t representing all possible Rust values. We do a first pass where we type all the code using user-provided Rocq types representing the Rust values of interest.
For example, for the Rust type:
pub enum Ordering {
Less = -1,
Equal = 0,
Greater = 1,
}
we will provide the Rocq type:
Module Ordering.
Inductive t : Set :=
| Less
| Equal
| Greater.
with an injection to go to the type of Rust values:
φ x :=
match x with
| Less =>
Value.StructTuple "core::cmp::Ordering::Less" [] [] []
| Equal =>
Value.StructTuple "core::cmp::Ordering::Equal" [] [] []
| Greater =>
Value.StructTuple "core::cmp::Ordering::Greater" [] [] []
end
The bulk of the type-checking phase is about showing that we can view all the untyped values as images of typed values, both for the inputs and outputs of functions, through the canonical injection defined for each type.
Here is the typing statement for the STATIC_CALL function, from the file revm_interpreter/instructions/links/contract/static_call.v:
Instance run_static_call
{WIRE H : Set} `{Link WIRE} `{Link H}
{WIRE_types : InterpreterTypes.Types.t} `{InterpreterTypes.Types.AreLinks WIRE_types}
{H_types : Host.Types.t} `{Host.Types.AreLinks H_types}
(run_InterpreterTypes_for_WIRE : InterpreterTypes.Run WIRE WIRE_types)
(run_Host_for_H : Host.Run H H_types)
(interpreter : '&mut (Interpreter.t WIRE WIRE_types))
(host : '&mut H) :
Run.Trait
instructions.contract.static_call [] [ Φ WIRE; Φ H ] [ φ interpreter; φ host ]
unit.
Proof.
constructor.
destruct (TryFrom_Uint_for_u64.method_try_from
(BITS := {| Integer.value := 256 |})
(LIMBS := {| Integer.value := 4 |})
).
run_symbolic.
Defined.
Global Opaque run_static_call.
Most of the proof is automated in the run_symbolic tactic, once we have properly declared the corresponding Rocq types and expressed the Rust traits as Rocq typeclasses.
Essentially, for a function from to , we show that:
with a constructive proof enabling the computation of from .
Memory
We do not print the code of the typed version of static_call, as this code can be extremely verbose! But we will step through it, using a semantics where we allocate local values on the stack, to show that the typed code is equivalent to the functional specification above. In this phase, we:
- Convert the control flow of Rust, with its
match,return, ... operators to Rocq ones; - Convert the use of stack-allocated (and sometimes heap-allocated) values to Rocq values, which are implicitly allocated, as this is a functional language.
Depending on the code, we will structure it using a state and/or error monad. The statement for the equivalence, from the file revm_interpreter/instructions/simulate/contract/static_call.v, is:
Lemma static_call_eq
{WIRE H : Set} `{Link WIRE} `{Link H}
{WIRE_types : InterpreterTypes.Types.t} `{InterpreterTypes.Types.AreLinks WIRE_types}
{H_types : Host.Types.t} `{Host.Types.AreLinks H_types}
(run_InterpreterTypes_for_WIRE : InterpreterTypes.Run WIRE WIRE_types)
(run_Host_for_H : Host.Run H H_types)
(IInterpreterTypes : InterpreterTypes.C WIRE_types)
(InterpreterTypesEq :
InterpreterTypes.Eq.t WIRE WIRE_types run_InterpreterTypes_for_WIRE IInterpreterTypes)
(IHost : Host.C H)
(HostEq : Host.Eq.t IHost)
(interpreter : Interpreter.t WIRE WIRE_types)
(host : H) :
let ref_interpreter := make_ref 0 in
let ref_host := make_ref 1 in
{{
SimulateM.eval_f (
run_static_call
run_InterpreterTypes_for_WIRE run_Host_for_H ref_interpreter ref_host
)
[interpreter; host]%stack 🌲
(
Output.Success tt,
let (interpreter, host) := static_call interpreter host in
[interpreter; host]%stack
)
}}.
where the function run_static_call is the typed version of the code extracted by rocq-of-rust, and static_all is our functional specification.
The notation:
{{ e 🌲 v }}
means that the monadic expression e evaluates to the purely functional value v.
The proof is done by stepping through each functional call or branching of the code of static_call. We could automate the proof further, but for now, we still step manually through the code for better control. Here is an extract from the proof:
eapply Run.Call. {
apply Impl_From_U256_for_FixedBytes_32.from_eq.
}
eapply Run.Call. {
apply Impl_Address.from_word_eq.
}
eapply Run.Call. {
apply TryFrom_Uint_for_u64.try_from_eq.
}
stepping through the function calls for:
B256::from(...)Address::from_word(...)u64::try_from(...)
✒️ Conclusion
We have seen how to formally verify the functional correctness of the Rust implementation for the STATIC_CALL instruction of the EVM using rocq-of-rust. These techniques are general, and enable the formal verification at scale of programs for a large subset of Rust, for arbitrary security properties using the theorem prover Rocq.
You want to secure critical applications? Discuss with us to know what is possible at contact@formal.land.